How To Change From Polar Coordinates To Cartesian

You can utilize both polar coordinates and Cartesian (10, y) coordinates (as well known as rectangular coordinates) at any time to describe the same location on the coordinate airplane. Sometimes you'll have an easier time using one course, and for this reason it'due south of import to know how to change between the ii. Cartesian coordinates are much meliorate suited for graphs of straight lines or simple curves. Polar coordinates can yield you a diversity of pretty, very circuitous graphs that you tin can't plot with Cartesian coordinates.

When irresolute to and from polar coordinates, your piece of work is often easier if you lot take all your angle measures in radians. You can make the change by using the conversion factor

You may choose, however, to leave your angle measures in degrees, which is fine as long as your calculator is in the right style.

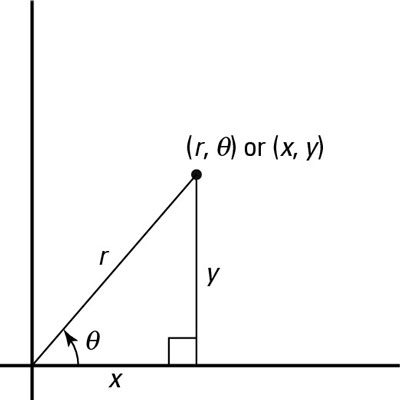
A polar and (x, y) coordinate mapped in the same plane.

Examine the point in this effigy, which illustrates a betoken mapped out in both (x, y) and

coordinates, allowing you to come across the relationship between them.

What exactly is the geometric relationship betwixt r,

x, and y? Look at how they're labeled on the graph — all parts of the same triangle!

Using right-triangle trigonometry, you know the following facts:

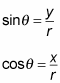
These equations simplify into two very important expressions for x and y in terms of r and

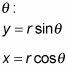
Furthermore, you lot can apply the Pythagorean theorem in the correct triangle to find the radius of the triangle if given x and y:

10 ² + y ² = r ²

One terminal equation allows you to detect the angle

information technology derives from the tangent of the angle:

So if you solve this equation for

you become the following expression:

With respect to the final equation, keep in mind that your calculator always returns a value of inverse tangent that puts

in the first or fourth quadrant. You need to await at your ten- and y-coordinates and decide whether that placement is actually correct for the trouble at manus. Your estimator doesn't look for tangent possibilities in the second and third quadrants, but that doesn't mean you don't have to!

Together, the four equations for r,

ten, and y allow you to change (x, y) coordinates into polar

coordinates and back once more anytime. For example, to modify the polar coordinate

to a rectangular coordinate, follow these steps:

1. Detect the x value.

   

   Apply the unit circle to get

   

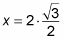
   which means that

   

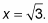
2. Find the y value.

   

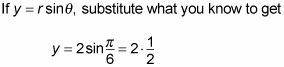
   which means that y = one.

3. Limited the values from Steps 1 and 2 as a coordinate signal.

   You discover that

   

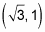
   is the answer equally a point.

Time for an instance in reverse. Given the point (–4, –4), find the equivalent polar coordinate:

1. Plot the (x, y) betoken first.

   

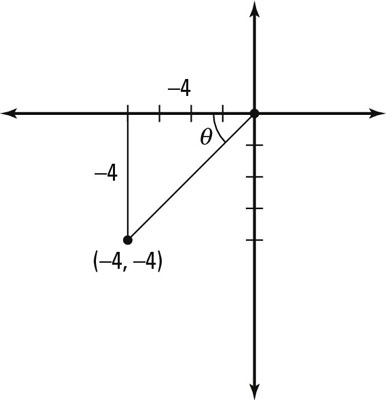
   An (x, y) coordinate changed to a polar coordinate.

   This figure shows the location of the point in quadrant III.

2. Find the r value.

   For this step, you use the Pythagorean theorem for polar coordinates: x ² + y ² = r ². Plug in what you know (ten = –4 and y = –4) to get (–4)² + (–four)² = r ², or

   

   

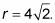
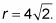
3. Find the value of

   

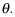
   Use the tangent ratio for polar coordinates:

   

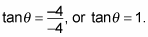
   The reference bending for this value is

   

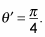
   You know from the figure that the bespeak is in the third quadrant, then

   

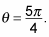
4. Express the values of Steps ii and 3 as a polar coordinate.

   You can say that

   

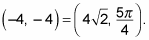
About This Article

This commodity is from the book:

• Geography For Dummies ,

Nigh the book author:

Jerry Mitchell is chairman of the Department of Geography at the University of South Carolina in Columbia, South Carolina, and an avid earth traveler who incorporates his personal stories and photos into his writing.

This article tin be found in the category:

• Pre-Calculus ,

Source: https://www.dummies.com/article/academics-the-arts/math/pre-calculus/how-to-change-between-polar-and-cartesian-coordinates-167712/

Posted by: gasparsible1980.blogspot.com

Share this post